|
|
< Free Open Study > |
|
4.5 More About Greediness and BacktrackingMany concerns (and benefits) of greediness are shared by both an NFA and a DFA. (A DFA doesn't support laziness, which is why we've concentrated on greediness up to this point.) I'd like to look at some ramifications of greediness for both, but with examples explained in terms of an NFA. The lessons apply to a DFA just as well, but not for the same reasons. A DFA is greedy, period, and there's not much more to say after that. It's very easy to use, but pretty boring to talk about. An NFA, however, is interesting because of the creative outlet its regex-directed nature provides. Besides lazy quantifiers, there are a variety of extra features an NFA can support, including lookaround, conditionals, backreferences, and atomic grouping. And on top of these, an NFA affords the regex author direct control over how a match is carried out, which can be a benefit when used properly, but it does create some efficiency-related pitfalls (discussed in Chapter 6.) Despite these differences, the match results are often similar. For the next few sections, I'll talk of both engine types, but describe effects in terms of the regexdir ected NFA. By the end of this chapter, you'll have a firm grasp of just when the results might differ, as well as exactly why. 4.5.1 Problems of GreedinessAs we saw with the last example,
Sometimes this can be a real pain. Consider a regex to match text wrapped in
double quotes. At first, you might want to write
The name "McDonald's" is said "makudonarudo" in Japanese Actually, since we understand the mechanics of matching, we don't need to guess,
because we know. Once the initial quote matches,
The name "McDonald's" is said "makudonarudo" in Japanese
which is obviously not the double-quoted string that was intended. This is one
reason why I caution against the overuse of
So, how can we have it match "McDonald's" only? The key is to realize that we
don't want "anything" between the quotes, but rather "anything except a quote." If
we use
The regex engine's basic approach with
Actually, there's could be one unexpected change, and that's because in most flavors,
4.5.2 Multi-Character "Quotes"In the first chapter, I talked a bit about matching HTML tags, such as the sequence
<B>very</B> that renders the "very" in bold if the browser can do so. Attempting
to match a <B>···</B> sequence seems similar to matching a quoted string, except the "quotes" in this case are the multi-character sequences <B> and </B>. Like the quoted string example, multiple sets of "quotes" cause problems if we use
With
Unfortunately, since the closing delimiter is more than one character, we can't
solve the problem with a negated class as we did with double-quoted strings. We
can't expect something like
4.5.3 Using Lazy QuantifiersThese problems arise because the standard quantifiers are greedy. Some NFAs support
lazy quantifiers (see Section 3.4.5.8), with *? being the lazy version of *. With that in mind, let's apply
···<B>Billions</B> and <B>Zillions</B> of suns··· After the initial
The
···<B>Billions</B> and <B>Zillions</B> of suns···
So, as we've seen, the greediness of star and friends can be a real boon at times,
while troublesome at others. Having non-greedy, lazy versions is wonderful, as
they allow you to do things that are otherwise very difficult (or even impossible).
Still, I've often seen inexperienced programmers use lazy quantifiers in inappropriate
situations. In fact, what we've just done may not be appropriate. Consider
applying
···<B>Billions</B> and <B>Zillions</B> of suns···
It matches as shown, and while I suppose it depends on the exact needs of the situation,
I would think that in this case that match is not desired. However, there's
nothing about
This is an excellent example of why a lazy quantifier is often not a good replacement
for a negated class. In the
However, if negative lookahead (see Section 3.4.3.6) is supported, you can use it to create something comparable to a negated class. Alone,
<B> # Match the opening <B>
( # Now, only as many of the following as needed . . .
(?! <B> ) # If not <B> . . .
. # . . . any character is okay
)*? #
</B> # . . . until the closing delimiter can match
With one adjustment to the lookahead, we can put the quantifier back to a normal greedy one, which may be less confusing to some:
<B> # Match the opening <B>
( # Now, only as many of the following as needed . . .
(?! < /? B> ) # If not <B>, and not </B> . . .
. # . . . any character is okay
)* #
</B> # . . . until the closing delimiter can match.
Now, the lookahead prohibits the main body to match beyond </B> as well as <B>, which eliminates the problem we tried to solve with laziness, so the laziness can be removed. This expression can still be improved; we'll see it again during the discussion on efficiency in Chapter 6 (see Section 6.6.7). 4.5.4 Greediness and Laziness Always Favor a MatchRecall the price display example from Chapter 2 (see Section 2.3.2). We'll examine this example in detail at a number of points during this chapter, so I'll recap the basic issue: due to floating-point representation problems, values that should have been "1.625" or "3.00" were sometimes coming out like "1.62500000002828" and "3.00000000028822". To fix this, I used $price =~ s/(\.\d\d[1-9]?)\d*/$1/; to lop off all but the first two or three decimal digits from the value stored in the
variable $price. The
I then noted:
So far so good, but let's consider what happens when the contents of the variable
$price is already well formed. When it is 27.625, the
This is the desired result, but wouldn't it be just a bit more efficient to do the
replacement only when it would have some real effect (that is, do the replacement
only when
$price =~ s/(\.\d\d[1-9]?)\d+/$1/ With crazy numbers like "1.62500000002828", it still works as before, but with
something such as "9.43", the trailing
In hindsight, the problem is really fairly simple. Picking up in the action once
What if
4.5.5 The Essence of Greediness, Laziness, and BacktrackingThe lesson of the preceding section is that it makes no difference whether there are greedy or lazy components to a regex; an overall match takes precedence over an overall non-match. This includes taking from what had been greedy (or giving to what had been lazy) if that's what is required to achieve a match, because when a "local failure" is hit, the engine keeps going back to the saved states (retracing steps to the piles of bread crumbs), trying the untested paths. Whether greedily or lazily, every possible path is tested before the engine admits failure. The order that the paths are tested is different between greedy and lazy quantifiers (after all, that's the whole point of having the two!), but in the end, if no match is to be found, it's known only after testing every possible path. If, on the other hand, there exists just one plausible match, both a regex with a greedy quantifier and one with a lazy quantifier find that match, although the series of paths they take to get there may be wildly different. In these cases, selecting greedy or lazy doesn't influence what is matched, but merely how long or short a path the engine takes to get there (which is an efficiency issue, the subject of Chapter 6). Finally, if there is more than one plausible match, understanding greediness, laziness,
and backtracking allows you to know which is selected. The
We know that
4.5.6 Possessive Quantifiers and Atomic GroupingThe '.625' example below shows important insights about NFA matching as we know it, and how with that particular example our naïve intents were thwarted. Some flavors do provide tools to help us here, but before looking at them, it's absolutely essential to fully understand the preceding section, "The Essence of Greediness, Laziness, and Backtracking." Be sure to review it if you have any doubts. So, continuing with the '.625' example and recalling what we really want to happen,
we know that if the matching can successfully get to the marked position in
Well, what if we could somehow eliminate that skip-me alternative (eliminate the
state that
It sounds like we have two conflicting desires, but thinking about it, what we
really want is to eliminate the skip-me alternative only if the match-me alternative
succeeds. That is, if
4.5.6.1 Atomic grouping with
|
at 'Subjec t' t'
| matching
 ^\w+ ^\w+ : : |
at which point the
 :
:![]() fails again, this time trying to match 't'. This backtrack-testfail
cycle happens all the way back to the oldest state:
fails again, this time trying to match 't'. This backtrack-testfail
cycle happens all the way back to the oldest state:
at 'S ubject' ubject'
| matching
 ^\w+ ^\w+ : : |
After the attempt from the final state fails, overall failure can finally be announced.
All that backtracking is a lot of work that after just a glance we know to be unnecessary.
If the colon can't match after the last letter, it certainly can't match one of
the letters the
 +
+![]() is forced to give up!
is forced to give up!
So, knowing that none of the states left by
 \w+
\w+![]() once it's finished, could possibly
lead to a match, we can save the regex engine the trouble of checking them:
once it's finished, could possibly
lead to a match, we can save the regex engine the trouble of checking them:
 \^(?>\w+):
\^(?>\w+):![]() By adding the atomic grouping, we use our global knowledge of the regex to enhance the local working of
By adding the atomic grouping, we use our global knowledge of the regex to enhance the local working of
 \w+
\w+![]() by having its saved states (which we
know to be useless) thrown away. If there is a match, the atomic grouping won't have mattered, but if there's not to be a match, having thrown away the useless
states lets the regex come to that conclusion more quickly. (An advanced implementation
may be able to apply this optimization for you automatically see Section 6.4.6.7.)
by having its saved states (which we
know to be useless) thrown away. If there is a match, the atomic grouping won't have mattered, but if there's not to be a match, having thrown away the useless
states lets the regex come to that conclusion more quickly. (An advanced implementation
may be able to apply this optimization for you automatically see Section 6.4.6.7.)
As we'll see in the Chapter 6 (see Section 6.6.6), this technique shows a very valuable use of atomic grouping, and I suspect it will become the most common use as well.
Possessive quantifiers are much like greedy quantifiers, but they never give up a
partial amount of what they've been able to match. Once a plus, for example, finishes
its run, it has created quite a few saved states, as we saw with the
 ^\w+
^\w+![]() example. A possessive plus simply throws those states away (or, more likely, doesn't bother creating them in the first place).
example. A possessive plus simply throws those states away (or, more likely, doesn't bother creating them in the first place).
As you might guess, possessive quantifiers are closely related to atomic grouping.
Something possessive like
 \w++
\w++![]() appears to match in the same way as
appears to match in the same way as
 (?>\w+)
(?>\w+)
![]() ;
one is just a notational convenience for the other.[8] With possessive quantifiers,
;
one is just a notational convenience for the other.[8] With possessive quantifiers,
 ^(?>\w+):
^(?>\w+):![]() can be rewritten as
can be rewritten as
 \w++:
\w++:![]() , and
, and
 (\.\d\d(?>[1-9]?))\d+
(\.\d\d(?>[1-9]?))\d+![]() can be rewritten as
can be rewritten as
 (\.\d\d[1-9]?+)\d+
(\.\d\d[1-9]?+)\d+![]() .
.
[8] A smart implementation may be able to make the possessive version a bit more efficient than its atomic-grouping counterpart (see Section 6.4.6.7).
Be sure to understand the difference between
 (?>M)+
(?>M)+![]() and
and
 (?>M+)
(?>M+)![]() . The first one throws away unused states created by
. The first one throws away unused states created by
 M
M![]() , which is not very useful since
, which is not very useful since
 M
M![]() doesn't create any states. The second one throws away unused states created by
doesn't create any states. The second one throws away unused states created by
 M+
M+![]() , which certainly can be useful.
, which certainly can be useful.
When phrased as a comparison between
 (?>M)+
(?>M)+![]() and
and
 (?>M+)
(?>M+)![]() , it's perhaps clear that the second one is the one comparable to
, it's perhaps clear that the second one is the one comparable to
 M++
M++![]() , but when converting something
more complex like
, but when converting something
more complex like
 (\\"|[^"])*+
(\\"|[^"])*+![]() from possessive quantifiers to atomic
grouping, it's tempting to just add '?>' to the parentheses that are already there:
from possessive quantifiers to atomic
grouping, it's tempting to just add '?>' to the parentheses that are already there:
 (?>\\"|[^"])*+
(?>\\"|[^"])*+![]() . The new expression might happen to achieve your goal, but be clear that is not comparable to the original possessive-quantifier version; it's as if
changing
. The new expression might happen to achieve your goal, but be clear that is not comparable to the original possessive-quantifier version; it's as if
changing
 M++
M++![]() to
to
 (?>M)+
(?>M)+![]() . Rather, to be comparable, remove the possessive plus,
and then wrap what remains in atomic grouping:
. Rather, to be comparable, remove the possessive plus,
and then wrap what remains in atomic grouping:
 (?>(\\"|[^"])*)
(?>(\\"|[^"])*)
![]() .
.
It might not be apparent at first, but lookaround (introduced in Chapter 2 see Section 2.3.5) is closely related to atomic grouping and possessive quantifiers. There are four types of lookaround: positive and negative flavors of lookahead and lookbehind. They simply test whether their subexpression can and can't match starting at the current location (lookahead), or ending at the current location (lookbehind).
Looking a bit deeper, how does lookaround work in our NFA world of saved states and backtracking? As a subexpression within one of the lookaround constructs is being tested, it's as if it's in its own little world. It saves states as needed, and backtracks as necessary. If the entire subexpression is able to match successfully, what happens? With positive lookaround, the construct, as a whole, is considered a success, and with negative lookaround, it's considered a failure. In either case, since the only concern is whether there's a match (and we just found out that, yes, there's a match), the "little world" of the match attempt, including any saved states that might have been left over from that attempt, is thrown away.
What about when the subexpression within the lookaround can't match? Since it's being applied in its "own little world," only states created within the current lookar ound construct are available. That is, if the regex finds that it needs to backtrack further, beyond where the lookaround construct started, it's found that the current subexpression can not match. For positive lookahead, this means failure, while for negative lookahead, it means success. In either case, there are no saved states left over (had there been, the subexpression match would not have finished), so there's no "little world" left to throw away.
So, we've seen that in all cases, once the lookaround construct has finished, there are no saved states left over from its application. Any states that might have been left over, such as in the case of successful positive lookahead, are thrown away.
Well, where else have we seen states being thrown away? With atomic grouping and possessive quantifiers, of course.
It's perhaps mostly academic for flavors that support atomic grouping, but can be
quite useful for those that don't: if you have positive lookahead, and if it supports capturing parentheses within the lookahead (most flavors do, but Tcl's lookahead, for example, does not), you can mimic atomic grouping and possessive quanti-
fiers.
 (?>
regex
)
(?>
regex
)![]() can be mimicked with
can be mimicked with
 (?=(
regex
))\1
(?=(
regex
))\1
![]() . For example, compare
. For example, compare
 ^(?>\w+):
^(?>\w+):![]() with
with
 ^(?=(\w+))\1:
^(?=(\w+))\1:![]() .
.
The lookahead version has
 \w+
\w+![]() greedily match as much as it can, capturing an
entire word. Because it's within lookahead, the intermediate states are thrown
away when it's finished (just as if, incidentally, it had been within atomic grouping).
Unlike atomic grouping, the matched word is not included as part of the
match (that's the whole point of lookahead), but the word does remain captured.
That's a key point because it means that when
greedily match as much as it can, capturing an
entire word. Because it's within lookahead, the intermediate states are thrown
away when it's finished (just as if, incidentally, it had been within atomic grouping).
Unlike atomic grouping, the matched word is not included as part of the
match (that's the whole point of lookahead), but the word does remain captured.
That's a key point because it means that when
 \1
\1![]() is applied, it's actually being applied to the very text that filled it, and it's certain to succeed. This extra step of applying
is applied, it's actually being applied to the very text that filled it, and it's certain to succeed. This extra step of applying
 \1
\1![]() is simply to move the regex past the matched word.
is simply to move the regex past the matched word.
This technique is a bit less efficient than real atomic grouping because of the extra
time required to rematch the text via
 \1
\1![]() . But, since states are thrown away, it fails
more quickly than a raw
. But, since states are thrown away, it fails
more quickly than a raw
 \w+:
\w+:![]() when the
when the
 :
:![]() can't match.
can't match.
How alternation works is an important point because it can work in fundamentally different ways with different regex engines. When alternation is reached, any number of the alternatives might be able to match at that point, but which will? Put another way, if more than one can match, which will? If it's always the one that matches the most text, one might say that alternation is greedy. If it's always the shortest amount of text, one might say it's lazy? Which (if either) is it?
Let's look at the Traditional NFA engine used in Perl, Java packages, .NET languages,
and many others (see Section 4.1.3). When faced with alternation, each alternative is checked in the right-to-left order given in the expression. With the example regex of
 ^(Subject|Date):•
^(Subject|Date):•![]() , when the
, when the
 Subject|Date
Subject|Date![]() alternation is reached, the first alternative,
alternation is reached, the first alternative,
 Subject
Subject![]() , is attempted. If it matches, the rest of the regex (the subsequent
, is attempted. If it matches, the rest of the regex (the subsequent
 :•
:•![]() ) is given a chance. If it turns out that it can't match, and if other alternatives
remain (in this case,
) is given a chance. If it turns out that it can't match, and if other alternatives
remain (in this case,
 Date
Date![]() ), the regex engine backtracks to try them. This is just another case of the regex engine backtracking to a point where untried options are still available. This continues until an overall match is achieved, or until all options (in this case, all alternatives) are exhausted.
), the regex engine backtracks to try them. This is just another case of the regex engine backtracking to a point where untried options are still available. This continues until an overall match is achieved, or until all options (in this case, all alternatives) are exhausted.
So, with that common Traditional NFA engine, what text is actually matched by
 tour|to|tournament
tour|to|tournament![]() when applied to the string 'three•tournaments•won' ? All
the alternatives are attempted (and fail) during attempts starting at each character
position until the transmission starts the attempt at 'three•
when applied to the string 'three•tournaments•won' ? All
the alternatives are attempted (and fail) during attempts starting at each character
position until the transmission starts the attempt at 'three• tournaments•won'.
This time, the first alternative,
tournaments•won'.
This time, the first alternative,
 tour
tour![]() , matches. Since the alternation is the last thing
in the regex, the moment the
, matches. Since the alternation is the last thing
in the regex, the moment the
 tour
tour![]() matches, the whole regex is done. The other alternatives are not even tried again.
matches, the whole regex is done. The other alternatives are not even tried again.
So, we see that alternation is neither greedy nor lazy, but ordered, at least for a Traditional NFA. This is more powerful than greedy alternation because it allows more control over just how a match is attempted — it allows the regex author to express "try this, then that, and finally try that, until you get a match."
Not all flavors have ordered alternation. DFAs and POSIX NFAs do have greedy
alternation, always matching with the alternative that matches the most text
(
 tournament
tournament![]() in this case). But, if you're using Perl, a .NET language, virtually any Java regex package, or any other system with a Traditional NFA engine (list see Section 4.1.3),
your alternation is ordered.
in this case). But, if you're using Perl, a .NET language, virtually any Java regex package, or any other system with a Traditional NFA engine (list see Section 4.1.3),
your alternation is ordered.
Let's revisit the
 (\.\d\d[1-9]?)\d*
(\.\d\d[1-9]?)\d*![]() example from Section 4.5.4. If we realize that
example from Section 4.5.4. If we realize that
 \.\d\d[1-9]?
\.\d\d[1-9]?![]() , in effect, says "allow either
, in effect, says "allow either
 \.\d\d
\.\d\d![]() or
or
 \.\d\d[1-9]
\.\d\d[1-9]![]() ", we can
rewrite the entire expression as
", we can
rewrite the entire expression as
 (\.\d\d|\.\d\d[1-9])\d*
(\.\d\d|\.\d\d[1-9])\d*![]() . (There is no compelling reason to make this change — it's merely a handy example.) Is this really the same as the original? If alternation is truly greedy, then it is, but the two are quite different with ordered alternation.
. (There is no compelling reason to make this change — it's merely a handy example.) Is this really the same as the original? If alternation is truly greedy, then it is, but the two are quite different with ordered alternation.
Let's consider it as ordered for the moment. The first alternative is selected and
tested, and if it matches, control passes to the
 \d*
\d*![]() that follows the alternation. If
there are digits remaining, the
that follows the alternation. If
there are digits remaining, the
 \d*
\d*![]() matches them, including any initial non-zero digit that was the root of the original example's problem (if you'll recall the original problem, that's a digit we want to match only within the parentheses, not by the
matches them, including any initial non-zero digit that was the root of the original example's problem (if you'll recall the original problem, that's a digit we want to match only within the parentheses, not by the
 \d*
\d*![]() after the parentheses). Also, realize that if the first alternative can't match,
the second alternative will certainly not be able to, as it begins with a copy of the
entire first alternative. If the first alternative doesn't match, though, the regex
engine nevertheless expends the effort for the futile attempt of the second.
after the parentheses). Also, realize that if the first alternative can't match,
the second alternative will certainly not be able to, as it begins with a copy of the
entire first alternative. If the first alternative doesn't match, though, the regex
engine nevertheless expends the effort for the futile attempt of the second.
Interestingly, if we swap the alternatives and use
 (\.\d\d[1-9]|\.\d\d)\d*
(\.\d\d[1-9]|\.\d\d)\d*![]() ,
we do effectively get a replica of the original greedy
,
we do effectively get a replica of the original greedy
 (\.\d\d[1-9]?)\d*
(\.\d\d[1-9]?)\d*![]() . The alternation has meaning in this case because if the first alternative fails due to the
trailing
. The alternation has meaning in this case because if the first alternative fails due to the
trailing
 [1-9]
[1-9]![]() , the second alternative still stands a chance. It's still ordered alternation,
but now we've selected the order to result in a greedy-type match.
, the second alternative still stands a chance. It's still ordered alternation,
but now we've selected the order to result in a greedy-type match.
When first distributing the
 [1-9]?
[1-9]?![]() to two alternatives, in placing the shorter one
first, we fashioned a non-greedy
to two alternatives, in placing the shorter one
first, we fashioned a non-greedy
 ?
?![]() of sorts. It ends up being meaningless in this
particular example because there is nothing that could ever allow the second alternative
to match if the first fails. I see this kind of faux-alternation often, and it is
invariably a mistake. In one book I've read,
of sorts. It ends up being meaningless in this
particular example because there is nothing that could ever allow the second alternative
to match if the first fails. I see this kind of faux-alternation often, and it is
invariably a mistake. In one book I've read,
 a*((ab)*|b*)
a*((ab)*|b*)
![]() is used as an example in explaining something about regex parentheses. It's a pointless example because
the first alternative,
is used as an example in explaining something about regex parentheses. It's a pointless example because
the first alternative,
 (ab)*
(ab)*![]() , can never fail, so any other alternatives are utterly
meaningless. You could add
, can never fail, so any other alternatives are utterly
meaningless. You could add
 a*((ab)*|b*|.*|partridge•in•a•pear•tree|[a-z])
a*((ab)*|b*|.*|partridge•in•a•pear•tree|[a-z])
and it wouldn't change the meaning a bit. The moral is that with ordered alternation, when more than one alternative can potentially match the same text, care must be taken when selecting the order of the alternatives.
Ordered alternation can be put to your advantage by allowing you to craft just the
match you want, but it can also lead to unexpected pitfalls for the unaware. Consider
matching a January date of the form 'Jan 31'. We need something more
sophisticated than, say,
 Jan•[0123][0-9]
Jan•[0123][0-9]![]() , as that allows "dates" such as 'Jan•00',
'Jan•39', and disallows, 'Jan•7'.
, as that allows "dates" such as 'Jan•00',
'Jan•39', and disallows, 'Jan•7'.
One way to match the date part is to attack it in sections. To match from the first
through the ninth, using
 0?[1-9]
0?[1-9]![]() allows a leading zero. Adding
allows a leading zero. Adding
 [12][0-9]
[12][0-9]![]() allows for the tenth through the 29th, and
allows for the tenth through the 29th, and
 3[01]
3[01]![]() rounds it out. Putting it all
together, we get
rounds it out. Putting it all
together, we get
 Jan•(0?[1-9]|[12][0-9]|3[01])
Jan•(0?[1-9]|[12][0-9]|3[01])
![]() .
.
Where do you think this matches in 'Jan 31 is Dad's birthday'? We want it to
match 'Jan 31', of course, but ordered alternation actually matches only 'Jan 3'.
Surprised? During the match of the first alternative,
 0?[1-9]
0?[1-9]![]() , the leading
, the leading
 0?
0?![]() fails,
but the alternative matches because the subsequent
fails,
but the alternative matches because the subsequent
 [1-9]
[1-9]![]() has no trouble matching
the 3. Since that's the end of the expression, the match is complete.
has no trouble matching
the 3. Since that's the end of the expression, the match is complete.
When the order of the alternatives is adjusted so that the alternative that can
potentially match a shorter amount of text is placed last, the problem goes away.
This works:
 Jan•([12][0-9]|3[01]|0?[1-9])
Jan•([12][0-9]|3[01]|0?[1-9])
![]() .
.
Another approach is
 Jan•(31|[123]0|[012]?[1-9])
Jan•(31|[123]0|[012]?[1-9])
![]() . Like the first solution,
this requires careful arrangement of the alternatives to avoid the problem. Yet, a
third approach is
. Like the first solution,
this requires careful arrangement of the alternatives to avoid the problem. Yet, a
third approach is
 Jan•(0[1-9]|[12][0-9]?|3[01]?|[4-9])
Jan•(0[1-9]|[12][0-9]?|3[01]?|[4-9])
![]() , which works properly regardless of the ordering. Comparing and contrasting these three expressions
can prove quite interesting (an exercise I'll leave for your free time, although
the sidebar below should be helpful).
, which works properly regardless of the ordering. Comparing and contrasting these three expressions
can prove quite interesting (an exercise I'll leave for your free time, although
the sidebar below should be helpful).
A Few Ways to Slice and Dice a DateA few approaches to the date-matching problem posed in Section 4.5.10.1. The calendar associated with each regex shows what can be matched by each alternative color-coded within the regex. 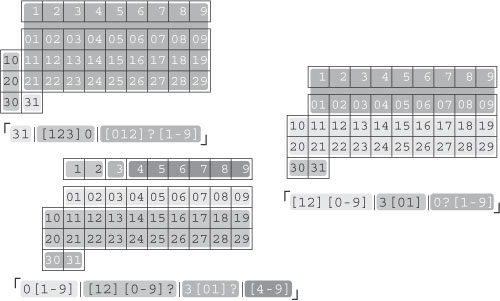
|
|
|
< Free Open Study > |
|