6.1 A Sobering Example

Let's start with an example that really shows how important a concern backtracking and efficiency can be. In Section 5.2.7, we came up with "(\\.| [^"\\])*" to match a quoted string, with internal quotes allowed if escaped. This regex works, but if it's used with an NFA engine, the alternation applied at each character is very inefficient. With every "normal" (non-escape, non-quote) character in the string, the engine has to test \\. , fail, and backtrack to finally match with [^"\\] . If used where efficiency matters, we would certainly like to be able to speed this regex up a bit.

6.1.1 A Simple Change—Placing Your Best Foot Forward

Since the average double-quoted string has more normal characters than escaped ones, one simple change is to swap the order of the alternatives, putting [^"\\] first and \\. second. By placing [^"\\] first, alternation backtracking need be done only when there actually is an escaped item in the string (and once for when the star fails, of course, since all alternatives must fail for the alternation as a whole to stop). Figure 6-1 illustrates this difference visually. The reduction of arrows in the bottom half represents the increased number of times when the first alternative matches. That means less backtracking.

Figure 1. Effects of alternative order (Traditional NFA)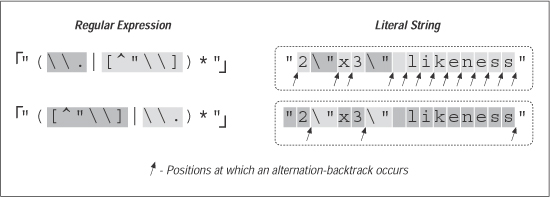

In evaluating this change, consider:

• Does this change benefit a Traditional NFA, POSIX NFA, or both?

• Does this change offer the most benefit when the text matches, when the match fails, or at all times?

Consider these questions and click here to check your answers. Make sure that you have a good grasp of the answers (and reasons) before continuing on to the next section.

6.1.2 Efficiency Verses Correctness

The most important question to ask when making any change for efficiency's sake is whether the change affects the correctness of a match. Reordering alternatives, as we did earlier, is okay only if the ordering is not relevant to the success of a match. Consider "(\\.|[^"])*" , which is an earlier (see Section 5.2.6.1) but flawed version of the regex in the previous section. It's missing the backslash in the negated character class, and so can match data that should not be matched. If the regex is only ever applied to valid data that should be matched, you'd never know of the problem. Thinking that the regex is good and reordering alternatives now to gain more efficiency, we'd be in real trouble. Swapping the alternatives so that [^"] is first actually ensures that it matches incorrectly every time the target has an escaped quote:

"You need a 2\"3\" photo."

So, be sure that you're comfortable with the correctness of a match before you worry too much about efficiency.

6.1.3 Advancing Further—Localizing the Greediness

Figure 6-1 makes it clear that in either expression, the star must iterate (or cycle, if you like) for each normal character, entering and leaving the alternation (and the parentheses) over and over. These actions involve overhead, which means extra work—extra work that we'd like to eliminate if possible.

Once while working on a similar expression, I realized that I could optimize it by taking into account that since [^"\\] matches the "normal" (non-quote, nonbackslash) case, using [^"\\]+ instead allows one iteration of (···)* to read as many normal characters as there are in a row. For strings without any escapes, this would be the entire string. This allows a match with almost no backtracking, and also reduces the star iteration to a bare minimum. I was very pleased with myself for making this discovery.

We'll look at this example in more depth later in this chapter, but a quick look at some statistics clearly shows the benefit. Figure 6-2 looks at this example for a Traditional NFA. In comparison to the original "(\\.|[^"\\]) *" (the top of the upper pair of Figure 6-2), alternation-related backtracks and star iterations are both reduced. The lower pair in Figure 6-2 illustrates that performance is enhanced even further when this change is combined with our previous reordering.

Figure 2. Effects of an added plus (Traditional NFA)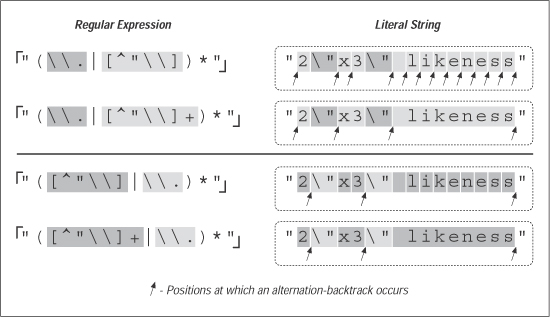

The big gain with the addition of plus is the resulting reduction in the number of alternation backtracks, and, in turn, the number of iterations by the star. The star quantifies a parenthesized subexpression, and each iteration entails some amount of overhead as the parentheses are entered and exited, because the engine needs to keep tabs on what text is matched by the enclosed subexpression. (This is discussed in depth later in this chapter.)

Table 6-1 is similar to the one in the answer block in Section 6.9.1, but with different expressions and has information about the number of iterations required by star. In each case, the number of individual tests and backtracks increases ever so slightly, but the number of cycles is drastically reduced. This is a big savings.

Table 6.1. Match Efficiency for a Traditional NFA

	Traditional NFA				POSIX NFA
	"([^"\\]|\\.)*"		"([^"\\]+|\\.)*"		either
	tests	b.t.	tests	b.t.	tests	b.t.
"2\"x3\" likeness"	32	14	22	4	48	30
"makudonarudo"	28	14	16	2	48	30
"very...99 more chars...long"	218	109	111	2	325	216
"No \"match\" here	124	86	124	86	124	86

6.1.4 Reality Check

Yes, I was quite pleased with myself for this discovery. However, as wonderful as this "enhancement" might seem, it is really a disaster waiting to happen. You'll notice that when extolling its virtues, I didn't give statistics for a POSIX NFA engine. If I had, you might have been surprised to find the "very•···• long" example requires over three hundred thousand million billion trillion backtracks (for the record, the actual count would be 324,518,553,658,426,726,783,156,020,576,256, or about 325 nonillion). Putting it mildly, that is a LOT of work. This would take well over 50 quintillion years, take or leave a few hundred trillion millennia. ^[1]

^[1] The reported time is an estimation based on other benchmarks; I did not actually run the test that long.

Quite surprising indeed! So, why does this happen? Briefly, it's because something in the regex is subject to both an immediate plus and an enclosing star, with nothing to differentiate which is in control of any particular target character. The resulting nondeterminism is the killer. The next section explains a bit more.

6.1.4.1 "Exponential" matches

Before adding the plus, [^"\\] was subject to only the star, and the number of possible ways for the effective ([^"\\])* to divvy up the line was limited. It matched one character, then another, and so forth, until each character in the target text had been matched at most one time. It may not have matched everything in the target, but at worst, the number of characters matched was directly proportional to the length of the target string. The possible amount of work rose in step with the length of the target string.

With the new regex's effective ([^"\\]+)* , the number of ways that the plus and star might divvy up the string explodes exponentially. If the target string is makudonarudo, should it be considered 12 iterations of the star, where each internal [^"\\]+ matches just one character (as might be shown by '')? Or perhaps one iteration of the star, where the internal [^"\\]+ matches everything (' makudonarudo ')? Or, perhaps 3 iterations of the star, where the internal [^"\\]+ matches 5, 3, and 4 characters respectively (''). Or perhaps 2, 2, 5, and 3 characters respectively (''). Or, perhaps...

Well, you get the idea — there are a lot of possibilities (4,096 in this 12-character example). For each extra character in the string, the number of possible combinations doubles, and the POSIX NFA must try them all before returning its answer. That's why these are called "exponential matches." Another appealing phrase I've heard for these types of matches is super-linear.

However called, it means backtracking, and lots of it! ^[2] Twelve characters' 4,096 combinations doesn't take long, but 20 characters' million-plus combinations take more than a few seconds. By 30 characters, the billion-plus combinations take hours, and by 40, it's well over a year. Obviously, this is not good.

^[2] For readers into such things, the number of backtracks done on a string of length n is 2 ⁿ⁺¹. The number of individual tests is 2 ⁿ⁺¹+ 2 ⁿ .

"Ah," you might think, "but a POSIX NFA is not all that common. I know my tool uses a Traditional NFA, so I'm okay." Well, the major difference between a POSIX and Traditional NFA is that the latter stops at the first full match. If there is no full match to be had, even a Traditional NFA must test every possible combination before it finds that out. Even in the short "No• \"match\"•here example from the previous answer block, 8,192 combinations must be tested before the failure can be reported.

When the regex engine crunches away on one of these neverending matches, the tool just seems to "lock up." The first time I experienced this, I thought I'd discover ed a bug in the tool, but now that I understand it, this kind of expression is part of my regular-expression benchmark suite, used to indicate the type of engine a tool implements:

• If one of these regexes is fast even with a non-match, it's likely a DFA.

• If it's fast only when there's a match, it's a Traditional NFA.

• If it's slow all the time, it's a POSIX NFA.

I used "likely" in the first bullet point because NFAs with advanced optimizations can detect and avoid these exponentially-painful neverending matches. (More on this later in this chapter see Section 6.4.6.7.) Also, we'll see a number of ways to augment or rewrite this expression such that it's fast for both matches and failures alike.

As the previous list indicates, at least in the absence of certain advanced optimizations, the relative performance of a regex like can tell you about the type of regex engine. That's why a form of this regex is used in the "Testing the Engine Type" section in Chapter 4 (see Section 4.1.5).

Certainly, not every little change has the disastrous effects we've seen with this example, but unless you know the work going on behind an expression, you will simply never know until you run into the problem. Toward that end, this chapter looks at the efficiency concerns and ramifications of a variety of examples. As with most things, a firm grasp of the underlying basic concepts is essential to an understanding of more advanced ideas, so before looking at ways to get around exponential matches, I'd like to review backtracking in explicit detail.